Sample Solution

IGNOU MST-015 Solved Assignment | June 2024 to June 2025 | Introduction to R Software | MSCAST Sample Solution

MST-015 Solved Assignment 2025

Question:-01

Attempt the following:
(a) Write the output of the following statements:

(i)

rep (X = C (T, F, T, F)

, times

= C (2, 1, 2, 3))

(ii)

5 % / % 3

; diag (3)

Answer:

(a) Write the output of the following statements:

(i) $rep (X = C (T, F, T, F)$ , times $= C (2, 1, 2, 3))$

In R, this statement would replicate the elements of the vector

X = c (T, F, T, F)

according to the times argument

c (2, 1, 2, 3)

The output would be a logical vector:

c (T, T, F, T, T, F, F, F)

(ii) $5 % / % 3$ ; diag (3)

In R, 5 %% 3 would calculate the remainder of 5 divided by 3, which is 2.

The diag(3) would create a 3×3 identity matrix.

The output would be:

[1] 2
     [,1] [,2] [,3]
[1,]    1    0    0
[2,]    0    1    0
[3,]    0    0    1

(b) Differentiate between the use of the sep and collapse arguments of the paste() function.

Answer:

In R, the paste() function is used for concatenating strings. The sep and collapse arguments serve different purposes within this function:

`sep` Argument:

The sep argument specifies the string that separates the elements to be concatenated. It is used to separate multiple pieces of text that you are joining together.

For example:

paste("Hello", "World", sep = " ")

Output: "Hello World"

Here, the sep argument puts a space between "Hello" and "World".

`collapse` Argument:

The collapse argument is used when you have a vector of strings that you want to collapse into a single string. It specifies the separator between elements within the resulting single string.

For example:

paste(c("Hello", "World"), collapse = " ")

Output: "Hello World"

Here, the collapse argument collapses the vector c("Hello", "World") into a single string, separating the elements by a space.

Key Differences:

sep is used to separate the elements that are being concatenated in a single call to paste().
collapse is used to collapse a vector of strings into a single string.
sep works between the elements in each function call, whereas collapse works on the entire vector to produce a single string.

Here’s an example that uses both sep and collapse:

paste(c("Hello", "World"), c("How", "are", "you"), sep = "-", collapse = " ")

Output: "Hello-How World-are Hello-you"

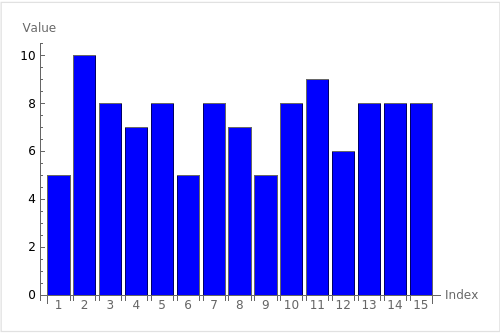
In this example, sep = "-" puts a hyphen between elements being concatenated ("Hello" with "How", "World" with "are", and so on). Then collapse = " " collapses the resulting vector into a single string, separating each element by a space.

(c) Write R commands to create a bar plot of the following data by using arguments of the used function for filling up the bars and to give labels to the axis:

5, 10, 8, 7, 8, 5, 8, 7, 5, 8, 9, 6, 8, 8, 8

Answer:
To fill the bars with a specific color and label the axes, you can use the col and xlab/ylab arguments, respectively.

Here’s an example R command to create a bar plot for the given data:

# Given data
data <- c(5, 10, 8, 7, 8, 5, 8, 7, 5, 8, 9, 6, 8, 8, 8)

# Create bar plot
barplot(data, 
        col = "blue",  # Fill color for bars
        xlab = "Index",  # Label for x-axis
        ylab = "Value"  # Label for y-axis
)

In this example, the bars are filled with the color blue. The x-axis is labeled as "Index" and the y-axis is labeled as "Value".

Here’s how the bar plot would look like when generated:

(d) Check whether the given loop is finite or infinite. If infinite, do the necessary changes in the written loop to make it finite.

x < - 0

repeat {

print (x \land 2)

x < - x + 1

(x < 5) print (x)}

Answer:

The given loop is infinite because there is no break statement to exit the loop. The if (x < 5) print(x) condition will only print the value of x when it is less than 5, but it won’t stop the loop from running indefinitely.

To make the loop finite, we can add a break statement with a condition to exit the loop. For example, you can break the loop when x reaches 5:

x <- 0
repeat {
  print(x^2)
  x <- x + 1
  if (x < 5) {
    print(x)
  } else {
    break
  }
}

In this modified version, the loop will terminate when x becomes 5, making it a finite loop.

Back to Course

Next Lesson

IGNOU MST-015 Solved Assignment | June 2024 to June 2025 | Introduction to R Software | MSCAST

Sample Solution

Question:-01

(a) Write the output of the following statements:

(i) rep ( X = C ( T , F , T , F ) rep ( X = C ( T , F , T , F ) rep(X=C(T,F,T,F)\operatorname{rep}(\mathrm{X}=\mathrm{C}(\mathrm{T}, \mathrm{F}, \mathrm{T}, \mathrm{F})rep(X=C(T,F,T,F), times = C ( 2 , 1 , 2 , 3 ) ) = C ( 2 , 1 , 2 , 3 ) ) =C(2,1,2,3))=\mathrm{C}(2,1,2,3))=C(2,1,2,3))

(ii) 5 % / % 3 5 % / % 3 5%//%35 \% / \% 35%/%3; diag (3)

sep Argument:

collapse Argument:

Key Differences:

(i) $rep (X = C (T, F, T, F)$ , times $= C (2, 1, 2, 3))$

(ii) $5 % / % 3$ ; diag (3)

`sep` Argument:

`collapse` Argument: