Free MCS-211 Solved Assignment | July 2025 | MCA_NEW, MCAOL | English & Hindi Medium | IGNOU

Question:-1(a)

Design and develop an efficient algorithm to find the list of prime numbers in the range 501 to 2000. What is the complexity of this algorithm?

Answer:

🧠 Step 1: Algorithm Design

1. Create a boolean list is_prime[0..2000], initialize all entries as True.
2. Mark is_prime[0] and is_prime[1] as False.
3. For $i=2$$i=2$i=2i = 2$i=2$ to $\sqrt{2000}\approx 44$$\sqrt{2000}\approx 44$sqrt2000~~44\sqrt{2000} \approx 44$\sqrt{2000}\approx 44$:
   • If is_prime[i] is True, mark all multiples of $i$$i$ii$i$ (from $i^2$$i^2$i^(2)i^2$i^2$ to 2000) as False.
4. Extract all primes between 501 and 2000 where is_prime[i] is True.

⚙️ Step 2: Pseudocode

n = 2000
is_prime = [True] * (n+1)
is_prime[0] = False
is_prime[1] = False

for i from 2 to int(sqrt(n)) + 1:
    if is_prime[i] is True:
        for j from i*i to n, step i:
            is_prime[j] = False

primes = []
for k from 501 to n:
    if is_prime[k]:
        primes.append(k)

⏱️ Step 3: Complexity Analysis

• Time Complexity: $O(n\log \log n)$$O(n\log \log n)$O(n log log n)O(n \log \log n)$O(n\log \log n)$
  (Efficient due to inner loop marking multiples only for primes)
• Space Complexity: $O(n)$$O(n)$O(n)O(n)$O(n)$
  (For the boolean list of size 2001)

✅ Why Efficient?

• Eliminates multiples of each prime starting from $i^2$$i^2$i^(2)i^2$i^2$, reducing redundant checks.
• Optimal for fixed ranges like 501–2000.

🧾 Example Output (First 5 primes in range):

• 503, 509, 521, 523, 541...

Question:-1(b)

Differentiate between Cubic-time and Factorial-time algorithms. Give example of one algorithm each for these two running times.

Answer:

⏱️ Cubic-Time vs. Factorial-Time Algorithms

🧊 Cubic-Time Algorithms

• Time Complexity: $O(n^3)$$O(n^3)$O(n^(3))O(n^3)$O(n^3)$
• Description: Running time grows proportional to the cube of the input size.
• Example:
  3 nested loops that each iterate $n$$n$nn$n$ times:

  for i in range(n):
      for j in range(n):
          for k in range(n):
              # constant-time operation
  
  Real-world example: Naive matrix multiplication for two $n\times n$$n\times n$n xx nn \times n$n\times n$ matrices.

🧮 Factorial-Time Algorithms

• Time Complexity: $O(n!)$$O(n!)$O(n!)O(n!)$O(n!)$
• Description: Running time grows factorial with input size (extremely fast).
• Example:
  Generating all permutations of $n$$n$nn$n$ distinct elements:

  def generate_permutations(arr, start=0):
      if start == len(arr):
          print(arr)
      for i in range(start, len(arr)):
          swap(arr, start, i)
          generate_permutations(arr, start+1)
          swap(arr, start, i)  # backtrack
  
  Real-world example: Solving the Traveling Salesman Problem via brute-force.

📊 Key Differences:

Question:-1(c)

Write an algorithm to multiply two square matrices of order $n\times n$$n\times n$n xx nn \times n$n\times n$. Also explain the time complexity of this algorithm.

Answer:

📝 Algorithm Steps:

1. Initialize a result matrix $C$$C$CC$C$ of size $n\times n$$n\times n$n xx nn \times n$n\times n$ with zeros.
2. For each row $i$$i$ii$i$ from 0 to $n-1$$n-1$n-1n-1$n-1$:
   • For each column $j$$j$jj$j$ from 0 to $n-1$$n-1$n-1n-1$n-1$:
     • Set $C[i][j]=0$$C[i][j]=0$C[i][j]=0C[i][j] = 0$C[i][j]=0$
     • For each index $k$$k$kk$k$ from 0 to $n-1$$n-1$n-1n-1$n-1$:
       • $C[i][j]+=A[i][k]\times B[k][j]$$C[i][j]+=A[i][k]\times B[k][j]$C[i][j]+=A[i][k]xx B[k][j]C[i][j] += A[i][k] \times B[k][j]$C[i][j]+=A[i][k]\times B[k][j]$
3. Return $C$$C$CC$C$

🧮 Example:

⏱️ Time Complexity:

• 3 nested loops, each running $n$$n$nn$n$ times.
• Total operations: $n\times n\times n=n^3$$n\times n\times n=n^3$n xx n xx n=n^(3)n \times n \times n = n^3$n\times n\times n=n^3$
• Time Complexity: $O(n^3)$$O(n^3)$O(n^(3))O(n^3)$O(n^3)$

Question:-1(d)

What are asymptotic bounds for analysis of efficiency of algorithms? Why are asymptotic bounds used? What are their shortcomings? Explain the Big O and Big $\mathrm{\Theta }$$\mathrm{\Theta }$Theta\Theta$\mathrm{\Theta }$ notation with the help of a diagram. Find the Big O-notation and $\mathrm{\Theta }$$\mathrm{\Theta }$Theta\Theta$\mathrm{\Theta }$-notation for the function: $$f(n)=100n^4+1000n^3+100000$$$$f(n)=100n^4+1000n^3+100000$$f(n)=100n^(4)+1000n^(3)+100000f(n) = 100n^4 + 1000n^3 + 100000$$f(n)=100n^4+1000n^3+100000$$

Answer:

📈 Asymptotic Bounds for Algorithm Efficiency

🔍 What are Asymptotic Bounds?

🎯 Why Use Asymptotic Bounds?

• Simplification: Ignore constants and focus on growth rate.
• Comparison: Easily compare algorithms based on scalability.
• Predictive: Help estimate performance for large inputs.

⚠️ Shortcomings:

• Ignore constants: May mislead for small inputs (e.g., $O(n^2)$$O(n^2)$O(n^(2))O(n^2)$O(n^2)$ might be faster than $O(n)$$O(n)$O(n)O(n)$O(n)$ for small $n$$n$nn$n$ if constants are large).
• Not exact: Do not give actual running time, only growth trend.
• Worst-case focus: Some bounds (e.g., Big O) often describe worst-case, not average or best-case.

📊 Big O and Big $\mathrm{\Theta }$$\mathrm{\Theta }$Theta\Theta$\mathrm{\Theta }$ Notation

• Big O ($O$$O$OO$O$): Upper bound (worst-case growth rate).
  Example: $f(n)=O(g(n))$$f(n)=O(g(n))$f(n)=O(g(n))f(n) = O(g(n))$f(n)=O(g(n))$ means $f$$f$ff$f$ grows at most as fast as $g$$g$gg$g$.
• Big Theta ($\mathrm{\Theta }$$\mathrm{\Theta }$Theta\Theta$\mathrm{\Theta }$): Tight bound (both upper and lower bounds).
  Example: $f(n)=\mathrm{\Theta }(g(n))$$f(n)=\mathrm{\Theta }(g(n))$f(n)=Theta(g(n))f(n) = \Theta(g(n))$f(n)=\mathrm{\Theta }(g(n))$ means $f$$f$ff$f$ grows exactly as fast as $g$$g$gg$g$ (within constant factors).

📉 Diagram Concept:

Growth Rate:
^
| Big O: f(n) ≤ c·g(n) (above curve)
| Big Θ: c₁·g(n) ≤ f(n) ≤ c₂·g(n) (sandwiched)
|
|----------------------------------> n

🧮 For $f(n)=100n^4+1000n^3+100000$$f(n)=100n^4+1000n^3+100000$f(n)=100n^(4)+1000n^(3)+100000f(n) = 100n^4 + 1000n^3 + 100000$f(n)=100n^4+1000n^3+100000$:

• Dominant term: $100n^4$$100n^4$100n^(4)100n^4$100n^4$ (highest power).
• Big O: $O(n^4)$$O(n^4)$O(n^(4))O(n^4)$O(n^4)$ (since $f(n)\le c\cdot n^4$$f(n)\le c\cdot n^4$f(n) <= c*n^(4)f(n) \leq c \cdot n^4$f(n)\le c\cdot n^4$ for $c=1000$$c=1000$c=1000c = 1000$c=1000$, $n\ge n_0$$n\ge n_0$n >= n_(0)n \geq n_0$n\ge n_0$).
• Big Θ: $\mathrm{\Theta }(n^4)$$\mathrm{\Theta }(n^4)$Theta(n^(4))\Theta(n^4)$\mathrm{\Theta }(n^4)$ (since $c_1{n}^4\le f(n)\le c_2{n}^4$$c_1{n}^4\le f(n)\le c_2{n}^4$c_(1)n^(4) <= f(n) <= c_(2)n^(4)c_1 n^4 \leq f(n) \leq c_2 n^4$c_1{n}^4\le f(n)\le c_2{n}^4$ for $c_1=100$$c_1=100$c_(1)=100c_1 = 100$c_1=100$, $c_2=1000$$c_2=1000$c_(2)=1000c_2 = 1000$c_2=1000$, $n\ge n_0$$n\ge n_0$n >= n_(0)n \geq n_0$n\ge n_0$).

✅ Final Notations:

• Big O: $O(n^4)$$O(n^4)$O(n^(4))O(n^4)$O(n^4)$
• Big Θ: $\mathrm{\Theta }(n^4)$$\mathrm{\Theta }(n^4)$Theta(n^(4))\Theta(n^4)$\mathrm{\Theta }(n^4)$

Question:-1(e)

Write and explain the Left to Right binary exponentiation algorithm. Demonstrate the use of this algorithm to compute the value of $3^{29}$$3^{29}$3^(29)3^{29}$3^{29}$. Show the steps of computation. Explain the worst-case complexity of this algorithm.

Answer:

🔢 Left-to-Right Binary Exponentiation Algorithm

📝 Algorithm Steps:

1. Convert $n$$n$nn$n$ to binary. Let $b$$b$bb$b$ be the binary digits.
2. Initialize result $r=1$$r=1$r=1r = 1$r=1$.
3. For each binary digit $b_i$$b_i$b_(i)b_i$b_i$ (from left to right):
   • $r=r\times r$$r=r\times r$r=r xx rr = r \times r$r=r\times r$ (square)
   • If $b_i=1$$b_i=1$b_(i)=1b_i = 1$b_i=1$:
     • $r=r\times a$$r=r\times a$r=r xx ar = r \times a$r=r\times a$ (multiply by base)
4. Return $r$$r$rr$r$.

🧮 Compute $3^{29}$$3^{29}$3^(29)3^{29}$3^{29}$:

• Binary of 29: $11101$$11101$1110111101$11101$ (left-to-right: 1,1,1,0,1)
• Steps:

⏱️ Worst-Case Complexity:

• Number of bits: $\lfloor {\log }_{2}n\rfloor +1$$\lfloor {\log }_{2}n\rfloor +1$|__log_(2)n __|+1\lfloor \log_2 n \rfloor + 1$\lfloor {\log }_{2}n\rfloor +1$
• Each step requires a square (and sometimes a multiply).
• Total operations: $O(\log n)$$O(\log n)$O(log n)O(\log n)$O(\log n)$ multiplications.

Question:-1(f)

Write and explain the Bubble sort algorithm. Discuss its best and worst-case time complexity.

Answer:

1. Start with an unsorted list of $n$$n$nn$n$ elements.
2. For each pass from $i=0$$i=0$i=0i = 0$i=0$ to $n-1$$n-1$n-1n-1$n-1$:
   • For each element from $j=0$$j=0$j=0j = 0$j=0$ to $n-i-1$$n-i-1$n-i-1n-i-1$n-i-1$:
     • Compare $arr[j]$$arr[j]$arr[j]arr[j]$arr[j]$ and $arr[j+1]$$arr[j+1]$arr[j+1]arr[j+1]$arr[j+1]$.
     • If $arr[j]>arr[j+1]$$arr[j]>arr[j+1]$arr[j] > arr[j+1]arr[j] > arr[j+1]$arr[j]>arr[j+1]$, swap them.
3. Repeat until no swaps are needed in a full pass.

• Pass 1: [2, 5, 1, 9]
• Pass 2: [2, 1, 5, 9]
• Pass 3: [1, 2, 5, 9] → Sorted

• Worst-case (reverse sorted): $O(n^2)$$O(n^2)$O(n^(2))O(n^2)$O(n^2)$
• Best-case (already sorted): $O(n)$$O(n)$O(n)O(n)$O(n)$ (with optimized check)
• Average-case: $O(n^2)$$O(n^2)$O(n^(2))O(n^2)$O(n^2)$

Question:-1(g)

What are the uses of recurrence relations? Solve the following recurrence relations using the Master’s method:

Answer:

📈 Uses of Recurrence Relations

• Analyzing algorithm efficiency (e.g., divide-and-conquer algorithms).
• Modeling problems in computer science, engineering, and mathematics.
• Predicting time/space complexity of recursive functions.

🧮 Master’s Method

🔹 (a) $T(n)=4T\left(\frac{n}{4}\right)+n$$T(n)=4T\left(\frac{n}{4}\right)+n$T(n)=4T((n)/(4))+nT(n) = 4T\left(\frac{n}{4}\right) + n$T(n)=4T\left(\frac{n}{4}\right)+n$

• $a=4$$a=4$a=4a = 4$a=4$, $b=4$$b=4$b=4b = 4$b=4$, $f(n)=n$$f(n)=n$f(n)=nf(n) = n$f(n)=n$
• $n^{{\log }_{b}a}=n^{{\log }_{4}4}=n^1=n$$n^{{\log }_{b}a}=n^{{\log }_{4}4}=n^1=n$n^(log _(b)a)=n^(log_(4)4)=n^(1)=nn^{\log_b a} = n^{\log_4 4} = n^1 = n$n^{{\log }_{b}a}=n^{{\log }_{4}4}=n^1=n$
• Since $f(n)=n=\mathrm{\Theta }(n^{{\log }_{b}a})$$f(n)=n=\mathrm{\Theta }(n^{{\log }_{b}a})$f(n)=n=Theta(n^(log _(b)a))f(n) = n = \Theta(n^{\log_b a})$f(n)=n=\mathrm{\Theta }(n^{{\log }_{b}a})$, Case 2 applies.
• Solution: $T(n)=\mathrm{\Theta }(n^{{\log }_{b}a}\log n)=\mathrm{\Theta }(n\log n)$$T(n)=\mathrm{\Theta }(n^{{\log }_{b}a}\log n)=\mathrm{\Theta }(n\log n)$T(n)=Theta(n^(log _(b)a)log n)=Theta(n log n)T(n) = \Theta(n^{\log_b a} \log n) = \Theta(n \log n)$T(n)=\mathrm{\Theta }(n^{{\log }_{b}a}\log n)=\mathrm{\Theta }(n\log n)$

🔹 (b) $T(n)=4T\left(\frac{3n}{4}\right)+n$$T(n)=4T\left(\frac{3n}{4}\right)+n$T(n)=4T((3n)/(4))+nT(n) = 4T\left(\frac{3n}{4}\right) + n$T(n)=4T\left(\frac{3n}{4}\right)+n$

• $a=4$$a=4$a=4a = 4$a=4$, $b=\frac{4}{3}$$b=\frac{4}{3}$b=(4)/(3)b = \frac{4}{3}$b=\frac{4}{3}$, $f(n)=n$$f(n)=n$f(n)=nf(n) = n$f(n)=n$
• $n^{{\log }_{b}a}=n^{{\log }_{4/3}4}$$n^{{\log }_{b}a}=n^{{\log }_{4/3}4}$n^(log _(b)a)=n^(log_(4//3)4)n^{\log_b a} = n^{\log_{4/3} 4}$n^{{\log }_{b}a}=n^{{\log }_{4/3}4}$.
  Note: ${\log }_{4/3}4>1$${\log }_{4/3}4>1$log_(4//3)4 > 1\log_{4/3} 4 > 1${\log }_{4/3}4>1$ (since $4/3<4$$4/3<4$4//3 < 44/3 < 4$4/3<4$), so $n^{{\log }_{b}a}$$n^{{\log }_{b}a}$n^(log _(b)a)n^{\log_b a}$n^{{\log }_{b}a}$ grows faster than $n$$n$nn$n$.
• Specifically, ${\log }_{4/3}4\approx 4.82$${\log }_{4/3}4\approx 4.82$log_(4//3)4~~4.82\log_{4/3} 4 \approx 4.82${\log }_{4/3}4\approx 4.82$, so $n^{{\log }_{b}a}\approx n^{4.82}$$n^{{\log }_{b}a}\approx n^{4.82}$n^(log _(b)a)~~n^(4.82)n^{\log_b a} \approx n^{4.82}$n^{{\log }_{b}a}\approx n^{4.82}$.
• Since $f(n)=n=O(n^{{\log }_{b}a-\epsilon })$$f(n)=n=O(n^{{\log }_{b}a-\epsilon })$f(n)=n=O(n^(log _(b)a-epsi))f(n) = n = O(n^{\log_b a - \varepsilon})$f(n)=n=O(n^{{\log }_{b}a-\epsilon })$ for some $\epsilon >0$$\epsilon >0$epsi > 0\varepsilon > 0$\epsilon >0$, Case 1 applies.
• Solution: $T(n)=\mathrm{\Theta }(n^{{\log }_{4/3}4})$$T(n)=\mathrm{\Theta }(n^{{\log }_{4/3}4})$T(n)=Theta(n^(log_(4//3)4))T(n) = \Theta(n^{\log_{4/3} 4})$T(n)=\mathrm{\Theta }(n^{{\log }_{4/3}4})$

✅ Final Answers:

• (a) $\mathrm{\Theta }(n\log n)$$\mathrm{\Theta }(n\log n)$Theta(n log n)\Theta(n \log n)$\mathrm{\Theta }(n\log n)$
• (b) $\mathrm{\Theta }(n^{{\log }_{4/3}4})$$\mathrm{\Theta }(n^{{\log }_{4/3}4})$Theta(n^(log_(4//3)4))\Theta(n^{\log_{4/3} 4})$\mathrm{\Theta }(n^{{\log }_{4/3}4})$ (exponential in log, but often simplified as $\mathrm{\Theta }(n^{4.82})$$\mathrm{\Theta }(n^{4.82})$Theta(n^(4.82))\Theta(n^{4.82})$\mathrm{\Theta }(n^{4.82})$)

Question:-2(a)

What is an Optimisation Problem? Explain with the help of an example. When would you use a Greedy Approach to solve optimisation problem? Formulate the Task Scheduling Problem as an optimisation problem and write a greedy algorithm to solve this problem. Also, solve the following fractional Knapsack problem using greedy approach. Show all the steps. Suppose there is a knapsack of capacity 20 Kg and the following 6 items are to be packed in it. The weight and profit of the items are as under:

Answer:

🎯 Optimization Problem

⚡ Greedy Approach

• The problem has the greedy choice property (local optimal choices lead to global optimum).
• It has optimal substructure (solution to subproblems helps solve the main problem).

📅 Task Scheduling as Optimization

• Each task has start and end times.
• Goal: Select maximum tasks without overlap.

1. Sort tasks by end time.
2. Select first task.
3. For each next task, if start ≥ last end time, select it.

🎒 Fractional Knapsack Problem

1. Sort by profit/weight (descending):
   Order: Item1 (6.0), Item4 (5.0), Item2 (4.0), Item3 (3.0), Item5 (2.0), Item6 (1.0)
2. Add items fully until capacity allows:
   • Item1: w=5, p=30 → cap=15, profit=30
   • Item4: w=4, p=20 → cap=11, profit=50
   • Item2: w=4, p=16 → cap=7, profit=66
   • Item3: w=6 > cap=7? Add fraction: (7/6)*18 = 21 → profit=66+21=87, cap=0

Question:-2(b)

Assuming that data to be transmitted consists of only characters ‘a’ to ‘g’, design the Huffman code for the following frequencies of character data. Show all the steps of building a Huffman tree. Also, show how a coded sequence using Huffman code can be decoded.

Answer:

🌳 Huffman Coding Steps

📊 Given Frequencies:

🔨 Step 1: Build Huffman Tree

1. Sort by frequency (ascending):
   a:5, f:7, e:8, c:10, d:15, b:25, g:30
2. Merge two smallest (a:5 + f:7 = 12):
   New list:
   e:8, c:10, 12, d:15, b:25, g:30
   (Node: a+f → 12)
3. Merge next two (e:8 + c:10 = 18):
   New list:
   12, 18, d:15, b:25, g:30
4. Merge 12 and d:15 = 27:
   New list:
   18, 27, b:25, g:30
5. Merge 18 and b:25 = 43:
   New list:
   27, 43, g:30
6. Merge 27 and g:30 = 57:
   New list:
   43, 57
7. Merge 43 and 57 = 100 (root)

🧩 Huffman Tree Structure:

         (100)
        /     \
     (43)     (57)
    /    \    /   \
 (18)   (25)b (27) (30)g
 /   \      /   \
(8)e (10)c (12) (15)d
         /   \
       (5)a  (7)f

🔤 Huffman Codes (Assign 0/0 to left/right):

• g: 11
• b: 01
• d: 101
• c: 001
• e: 000
• a: 1000
• f: 1001

🔍 Decoding a Coded Sequence

• Start at root.
• Read bits:
  • 11 → g
  • 01 → b
  • 10 → partial (d? Wait, d=101, so need more)
  • 101 → d
  • 000 → e

✅ Summary:

• Huffman codes are variable-length, prefix-free.
• Decoding traverses tree until a leaf is reached.

Question:-2(c)

Explain the Merge procedure of the Merge Sort algorithm. Demonstrate the use of recursive Merge sort algorithm for sorting the following data of size 8: [19, 18, 16, 12, 11, 10, 9, 8]. Compute the complexity of Merge Sort algorithm.

Answer:

🔄 Merge Procedure in Merge Sort

1. Comparing the smallest elements of each subarray.
2. Taking the smaller element and placing it in the result.
3. Repeating until all elements are merged.

🧩 Example Merge:

🧠 Recursive Merge Sort on [19,18,16,12,11,10,9,8]

• [19,18,16,12] and [11,10,9,8]
• [19,18] and [16,12]; [11,10] and [9,8]
• [19] and [18]; [16] and [12]; [11] and [10]; [9] and [8]

• Merge [19] & [18] → [18,19]
• Merge [16] & [12] → [12,16]
• Merge [11] & [10] → [10,11]
• Merge [9] & [8] → [8,9]

• Merge [18,19] & [12,16] → [12,16,18,19]
• Merge [10,11] & [8,9] → [8,9,10,11]

• Merge [12,16,18,19] & [8,9,10,11] → [8,9,10,11,12,16,18,19]

⏱️ Complexity Analysis

• Time: $O(n\log n)$$O(n\log n)$O(n log n)O(n \log n)$O(n\log n)$ in all cases (split and merge steps).
• Space: $O(n)$$O(n)$O(n)O(n)$O(n)$ for temporary arrays.

Question:-2(d)

Explain the divide and conquer approach of multiplying two large integers. Compute the time complexity of this approach. Also, explain the binary search algorithm and find its time complexity.

Answer:

🧮 Divide and Conquer for Large Integer Multiplication

📦 Approach:

⏱️ Time Complexity:

• Recurrence: $T(n)=4T(n/2)+O(n)$$T(n)=4T(n/2)+O(n)$T(n)=4T(n//2)+O(n)T(n) = 4T(n/2) + O(n)$T(n)=4T(n/2)+O(n)$
• Using Master Theorem: $O(n^{{\log }_{2}4})=O(n^2)$$O(n^{{\log }_{2}4})=O(n^2)$O(n^(log_(2)4))=O(n^(2))O(n^{\log_2 4}) = O(n^2)$O(n^{{\log }_{2}4})=O(n^2)$
  (Same as school method, but Karatsuba improves to $O(n^{1.58})$$O(n^{1.58})$O(n^(1.58))O(n^{1.58})$O(n^{1.58})$)

🔍 Binary Search Algorithm

🎯 Steps:

1. Start with sorted array.
2. Compare target with middle element.
3. If equal, return index.
4. If target < middle, search left half.
5. If target > middle, search right half.
6. Repeat until found or subarray size becomes 0.

⏱️ Time Complexity:

• Each step halves the search space.
• Recurrence: $T(n)=T(n/2)+O(1)$$T(n)=T(n/2)+O(1)$T(n)=T(n//2)+O(1)T(n) = T(n/2) + O(1)$T(n)=T(n/2)+O(1)$
• Solution: $O(\log n)$$O(\log n)$O(log n)O(\log n)$O(\log n)$

• Integer Multiplication: $O(n^2)$$O(n^2)$O(n^(2))O(n^2)$O(n^2)$ with divide and conquer (baseline).
• Binary Search: $O(\log n)$$O(\log n)$O(log n)O(\log n)$O(\log n)$ for sorted arrays.

Question:-2(e)

Explain the Topological sorting with the help of an example. Also, explain the algorithm of finding strongly connected components in a directed Graph.

Answer:

🔝 Topological Sorting

📌 Example:

• $A,B,C,D,E$$A,B,C,D,E$A,B,C,D,EA, B, C, D, E$A,B,C,D,E$
• $B,A,D,C,E$$B,A,D,C,E$B,A,D,C,EB, A, D, C, E$B,A,D,C,E$
  (Note: $A$$A$AA$A$ and $B$$B$BB$B$ have no constraints relative to each other)

⚙️ Algorithm (Kahn’s Algorithm):

1. Compute in-degree (number of incoming edges) for each vertex.
2. Enqueue all vertices with in-degree 0.
3. While queue not empty:
   • Dequeue a vertex $u$$u$uu$u$, add it to the topological order.
   • For each neighbor $v$$v$vv$v$ of $u$$u$uu$u$:
     • Reduce in-degree of $v$$v$vv$v$ by 1.
     • If in-degree becomes 0, enqueue $v$$v$vv$v$.

🔄 Strongly Connected Components (SCCs)

⚙️ Algorithm (Kosaraju’s Algorithm):

1. Step 1: Perform DFS on the graph to compute finishing times.
2. Step 2: Compute the transpose graph (reverse all edges).
3. Step 3: Perform DFS on the transpose graph in decreasing order of finishing times.

📌 Example:

• $\{A,B,C\}$$\{A,B,C\}${A,B,C}\{A, B, C\}$\{A,B,C\}$ (cycle)
• $\{D,E\}$$\{D,E\}${D,E}\{D, E\}$\{D,E\}$ (cycle)

Question:-3(a)

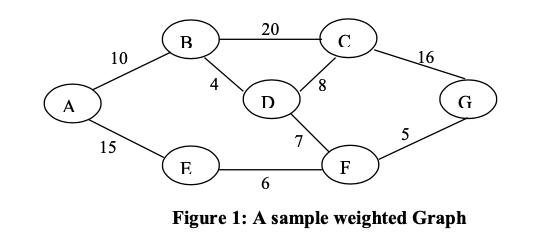
Write the Prim’s algorithm to find the minimum cost spanning tree of a graph. Also, find the time complexity of Prim’s algorithm. Demonstrate the use of Kruskal’s algorithm and Prim’s algorithm to find the minimum cost spanning tree for the Graph given in Figure 1. Show all the steps.

Answer:

Prim’s Algorithm for Minimum Spanning Tree (MST)

Pseudocode

PrimMST(Graph G = (V, E), weights w: E → R, start_vertex s ∈ V):
    // Initialize
    MST = empty set  // Set of edges in the MST
    inMST = array of size |V|, initialized to False  // Tracks vertices in MST
    key = array of size |V|, initialized to infinity  // Minimum weight to connect to MST
    parent = array of size |V|, initialized to -1  // Parent in MST
    
    key[s] = 0  // Start from s
    
    // Use a priority queue (min-heap) to select minimum key vertex
    PQ = priority_queue of all vertices, keyed by key values
    
    while PQ is not empty:
        u = extract_min(PQ)  // Vertex with smallest key not in MST
        inMST[u] = True
        
        for each neighbor v of u:
            if not inMST[v] and w(u, v) < key[v]:
                key[v] = w(u, v)
                parent[v] = u
                update PQ with new key for v  // Decrease key operation
    
    // Construct MST edges from parent array (excluding root)
    for each v in V except s:
        add edge (parent[v], v) to MST with weight key[v]
    
    return MST

How to Arrive at the Solution

• Initialization: Start with a single vertex (arbitrary choice) in the MST. Set its key to 0 and others to infinity.
• Growth: Use a priority queue to always pick the next vertex outside the MST with the smallest connecting edge. Update keys for its neighbors if a better edge is found.
• Termination: Continues until all vertices are included (|V| - 1 edges in MST).
• This ensures the MST is built by always choosing the locally optimal (smallest) safe edge, guaranteeing global optimality for undirected graphs with positive weights (by the greedy choice property).

Time Complexity

• With a binary heap for the priority queue and adjacency list representation:
  • Extract-min: O(V log V) total (V extractions).
  • Decrease-key: O(E log V) total (up to E updates).
  • Overall: O((V + E) log V), which simplifies to O(E log V) since E ≥ V-1 in connected graphs.
• For dense graphs (E ≈ V²) using an adjacency matrix without heap: O(V²).
• The O(E log V) is common for sparse graphs.

Demonstration on the Given Graph

• A-B: 10
• A-E: 15
• B-C: 20
• B-D: 4
• C-D: 8
• C-G: 16
• D-F: 7
• E-F: 6
• F-G: 5

Kruskal’s Algorithm Demonstration

1. Sort edges by weight:
   (B-D: 4), (F-G: 5), (E-F: 6), (D-F: 7), (C-D: 8), (A-B: 10), (A-E: 15), (C-G: 16), (B-C: 20).
2. Initialize Union-Find: Each vertex is its own component: {A}, {B}, {C}, {D}, {E}, {F}, {G}.
3. Add edges one by one:
   • Add B-D: 4 (connects {B} and {D} → {B,D}; no cycle). MST: {B-D}, cost = 4.
   • Add F-G: 5 (connects {F} and {G} → {F,G}; no cycle). MST: {B-D, F-G}, cost = 9.
   • Add E-F: 6 (connects {E} and {F,G} → {E,F,G}; no cycle). MST: {B-D, F-G, E-F}, cost = 15.
   • Add D-F: 7 (connects {B,D} and {E,F,G} → {B,D,E,F,G}; no cycle). MST: {B-D, F-G, E-F, D-F}, cost = 22.
   • Add C-D: 8 (connects {C} and {B,D,E,F,G} → {B,C,D,E,F,G}; no cycle). MST: {B-D, F-G, E-F, D-F, C-D}, cost = 30.
   • Add A-B: 10 (connects {A} and {B,C,D,E,F,G} → {A,B,C,D,E,F,G}; no cycle). MST: {B-D, F-G, E-F, D-F, C-D, A-B}, cost = 40.
   • Skip A-E: 15 (A and E already connected; cycle).
   • Skip C-G: 16 (C and G already connected; cycle).
   • Skip B-C: 20 (B and C already connected; cycle).
4. Final MST: Edges {A-B: 10, B-D: 4, C-D: 8, D-F: 7, E-F: 6, F-G: 5}. Total cost: 40.

How to Arrive at the Solution (Kruskal’s)

• Sorting ensures we consider smallest edges first.
• Union-Find efficiently checks cycles (find if roots are same) and merges components (union by rank/path compression for O(α(E)) amortized time, where α is inverse Ackermann).
• Stop after |V|-1 = 6 edges. The greedy choice avoids cycles while minimizing total weight.

Prim’s Algorithm Demonstration

1. Initialize:
   • inMST: All False.
   • key: All ∞ except key[A] = 0.
   • parent: All -1.
   • PQ: All vertices, min is A.
2. Iterations:
   • Extract A (key=0). inMST[A]=True. Update neighbors: key[B]=10 (parent[B]=A), key[E]=15 (parent[E]=A).
   • Extract B (min key=10). inMST[B]=True. Update: key[D]=4 (parent[D]=B), key[C]=20 (parent[C]=B). (Ignore A.)
   • Extract D (min key=4). inMST[D]=True. Update: key[C]=8 (better than 20, parent[C]=D), key[F]=7 (parent[F]=D). (Ignore B.)
   • Extract F (min key=7). inMST[F]=True. Update: key[E]=6 (better than 15, parent[E]=F), key[G]=5 (parent[G]=F). (Ignore D.)
   • Extract G (min key=5). inMST[G]=True. Update: key[C]=8 (no change). (Ignore F.)
   • Extract E (min key=6). inMST[E]=True. Update: No better updates. (Ignore A, F.)
   • Extract C (min key=8). inMST[C]=True. No better updates. (Ignore B, D, G.)
3. Final MST: From parents: B←A (10), D←B (4), F←D (7), G←F (5), E←F (6), C←D (8). Edges {A-B: 10, B-D: 4, D-C: 8, D-F: 7, F-E: 6, F-G: 5}. Total cost: 40.

How to Arrive at the Solution (Prim’s)

• Start from A and grow the tree by always adding the cheapest edge to the fringe (priority queue handles this).
• Updates ensure each vertex's key is the minimum possible at each step.
• Different starting vertex (e.g., G) may yield a different tree but same cost, as the algorithm is correct for connected graphs.

Question:-3(b)

Write the Dijkstra’s shortest path algorithm. Also, find the time complexity of this shortest path algorithm. Find the shortest paths from the vertex ‘A’ using Dijkstra’s shortest path algorithm for the graph given in Figure 1. Show all the steps of computation.

Answer:

Dijkstra’s Shortest Path Algorithm

Pseudocode

Dijkstra(Graph G = (V, E), weights w: E → R ≥ 0, source s ∈ V):
    // Initialize
    dist = array of size |V|, initialized to infinity  // Shortest distance from s
    prev = array of size |V|, initialized to -1  // Previous vertex in path
    dist[s] = 0
    
    // Priority queue (min-heap) for vertices not yet finalized, keyed by dist
    PQ = priority_queue of all vertices, keyed by dist values
    
    while PQ is not empty:
        u = extract_min(PQ)  // Vertex with smallest dist
        
        for each neighbor v of u:
            if dist[v] > dist[u] + w(u, v):
                dist[v] = dist[u] + w(u, v)
                prev[v] = u
                update PQ with new dist for v  // Decrease key operation
    
    // To reconstruct path to a target t: backtrack from t using prev until s
    return dist, prev

Time Complexity

• With a binary heap for the priority queue and adjacency list representation:
  • Extract-min: O(V log V) total (V extractions).
  • Decrease-key: O(E log V) total (up to E updates).
  • Overall: O((V + E) log V), which simplifies to O(E log V) since E ≥ V-1 in connected graphs.
• For dense graphs (E ≈ V²) using a simple array for minimum selection (no heap): O(V²).
• The O(E log V) variant is common for sparse graphs and assumes a heap that supports efficient decrease-key (e.g., binary or Fibonacci heap; Fibonacci reduces to amortized O(E + V log V)).

Demonstration on the Given Graph: Shortest Paths from A

Initialization

• dist: [A: 0, B: ∞, C: ∞, D: ∞, E: ∞, F: ∞, G: ∞]
• prev: [all -1]
• PQ: All vertices (min keyed on dist; initially A at 0, others ∞)

Step-by-Step Computation

Final Shortest Distances from A

• A: 0
• B: 10
• C: 22
• D: 14
• E: 15
• F: 21
• G: 26

Shortest Paths from A (Reconstructed using prev)

• To A: A (distance 0)
• To B: A → B (distance 10)
• To C: A → B → D → C (distance 10 + 4 + 8 = 22)
• To D: A → B → D (distance 10 + 4 = 14)
• To E: A → E (distance 15)
• To F: A → B → D → F (distance 10 + 4 + 7 = 21)
  Note: Alternative path A → E → F (15 + 6 = 21) has the same distance; the algorithm found one via D.
• To G: A → B → D → F → G (distance 10 + 4 + 7 + 5 = 26)
  Note: Alternative A → E → F → G (15 + 6 + 5 = 26) equivalent.

How to Arrive at the Solution

• Initialization: Set source distance to 0, others to infinity.
• Relaxation: For each extracted u, check if a shorter path to v exists via u; update if so.
• Priority Queue: Ensures the next u is always the one with the current smallest dist (greedy choice).
• Correctness: Relies on non-negative weights; once a vertex is extracted, its dist is finalized (no shorter path can be found later).
• The steps guarantee optimality by the invariant: at each extraction, dist[u] is the true shortest path.

Question:-3(c)

Explain the algorithm to find the optimal Binary Search Tree. Demonstrate this algorithm to find the Optimal Binary Search Tree for the following probability data (where $p_i$$p_i$p_(i)p_i$p_i$ represents the probability that the search will be for the key node $k_i$$k_i$k_(i)k_i$k_i$, whereas $q_i$$q_i$q_(i)q_i$q_i$ represents that the search is for dummy node $d_i$$d_i$d_(i)d_i$d_i$. Make suitable assumptions, if any):

Answer:

Algorithm to Find the Optimal Binary Search Tree

• Let $e[i][j]$$e[i][j]$e[i][j]e[i][j]$e[i][j]$ be the minimum expected search cost for the subtree containing keys $k_i$$k_i$k_(i)k_i$k_i$ to $k_j$$k_j$k_(j)k_j$k_j$ (for $1\le i\le j\le n$$1\le i\le j\le n$1 <= i <= j <= n1 \leq i \leq j \leq n$1\le i\le j\le n$).
• Let $w[i][j]$$w[i][j]$w[i][j]w[i][j]$w[i][j]$ be the total probability mass for this subtree: $w[i][j]=\sum _{l=i}^j{p}_l+\sum _{l=i-1}^j{q}_l$$w[i][j]=\sum _{l=i}^j p_l+\sum _{l=i-1}^j q_l$w[i][j]=sum_(l=i)^(j)p_(l)+sum_(l=i-1)^(j)q_(l)w[i][j] = \sum_{l=i}^j p_l + \sum_{l=i-1}^j q_l$w[i][j]=\sum _{l=i}^j{p}_l+\sum _{l=i-1}^j{q}_l$.
• Base cases:
  • For empty subtrees ($j=i-1$$j=i-1$j=i-1j = i-1$j=i-1$): $e[i][i-1]=0$$e[i][i-1]=0$e[i][i-1]=0e[i][i-1] = 0$e[i][i-1]=0$, $w[i][i-1]=0$$w[i][i-1]=0$w[i][i-1]=0w[i][i-1] = 0$w[i][i-1]=0$ (for $i=1$$i=1$i=1i = 1$i=1$ to $n+1$$n+1$n+1n+1$n+1$).
• Recurrence:
  • $w[i][j]=w[i][j-1]+p_j+q_j$$w[i][j]=w[i][j-1]+p_j+q_j$w[i][j]=w[i][j-1]+p_(j)+q_(j)w[i][j] = w[i][j-1] + p_j + q_j$w[i][j]=w[i][j-1]+p_j+q_j$
  • $e[i][j]=\underset{r=i}{\overset{j}{min}}(e[i][r-1]+e[r+1][j]+w[i][j])$$e[i][j]=\underset{r=i}{\overset{j}{min}} \left(e[i][r-1]+e[r+1][j]+w[i][j]\right)$e[i][j]=min_(r=i)^(j)(e[i][r-1]+e[r+1][j]+w[i][j])e[i][j] = \min_{r=i}^j \left( e[i][r-1] + e[r+1][j] + w[i][j] \right)$e[i][j]=\underset{r=i}{\overset{j}{min}}(e[i][r-1]+e[r+1][j]+w[i][j])$
• To track the tree structure, record $\text{root}[i][j]$$\text{root}[i][j]$"root"[i][j]\text{root}[i][j]$\text{root}[i][j]$ as the $r$$r$rr$r$ that achieves the minimum.
• Compute in order of increasing subtree size $l=j-i+1$$l=j-i+1$l=j-i+1l = j - i + 1$l=j-i+1$ (from 1 to $n$$n$nn$n$).
• The optimal cost is $e[1][n]$$e[1][n]$e[1][n]e[1][n]$e[1][n]$; the tree is constructed recursively using the root table.

Time Complexity

• The DP fills an $O(n^2)$$O(n^2)$O(n^(2))O(n^2)$O(n^2)$ table, and for each $e[i][j]$$e[i][j]$e[i][j]e[i][j]$e[i][j]$, it tries $O(n)$$O(n)$O(n)O(n)$O(n)$ choices for $r$$r$rr$r$.
• Total: $O(n^3)$$O(n^3)$O(n^(3))O(n^3)$O(n^3)$.