Course Code: BMTC-134
Assignment Code: BMTC-134/TMA/2023
Maximum Marks: 100

\section{PART-A (MM: 50 Marks)}

(To be done after studying Blocks 1 and 2.)

1. Which of the following statements are true? Give reasons for your answers.

i) If a group \(G\) is isomorphic to one of its proper subgroups, then \(G=\mathbb{Z}\).

ii) If \(\mathrm{x}\) and \(\mathrm{y}\) are elements of a non-abelian group \((\mathrm{G}, *)\) such that \(\mathrm{x} * \mathrm{y}=\mathrm{y} * \mathrm{x}\), then \(\mathrm{x}=\mathrm{e}\) or \(\mathrm{y}=\mathrm{e}\), where \(\mathrm{e}\) is the identity of \(\mathrm{G}\) with respect to \(*\).

iii) There exists a unique non-abelian group of prime order.

iv) If \((a, b) \in A \times A\), where \(A\) is a group, then \(o((a, b))=o(a) o(b)\).

v) If \(\mathrm{H}\) and \(\mathrm{K}\) are normal subgroups of a group \(\mathrm{G}\), then \(h k=k h \forall \mathrm{h} \in \mathrm{H}, \mathrm{k} \in \mathrm{K}\).

2. a) Prove that every non-trivial subgroup of a cyclic group has finite index. Hence prove that \((\mathbb{Q},+)\) is not cyclic.

b) Let \(\mathrm{G}\) be an infinite group such that for any non-trivial subgroup \(\mathrm{H}\) of \(G,|G: H|<\infty\). Then prove that

i) \(\mathrm{H} \leq \mathrm{G} \Rightarrow \mathrm{H}=\{\mathrm{e}\}\) or \(\mathrm{H}\) is infinite;

ii) If \(g \in G, g \neq e\), then \(o(g)\) is infinite.

c) Prove that a cyclic group with only one generator can have at most 2 elements.

3. a) Using Cayley’s theorem, find the permutation group to which a cyclic group of order 12 is isomorphic.

b) Let \(\tau\) be a fixed odd permutation in \(\mathrm{S}_{10}\). Show that every odd permutation in \(\mathrm{S}_{10}\) is a product of \(\tau\) and some permutation in \(\mathrm{A}_{10}\).

c) List two distinct cosets of \(\langle\mathrm{r}\rangle\) in \(\mathrm{D}_{10}\), where \(\mathrm{r}\) is a reflection in \(\mathrm{D}_{10}\).

d) Give the smallest \(n \in \mathbb{N}\) for which \(A_{n}\) is non-abelian. Justify your answer.

4. Use the Fundamental Theorem of Homomorphism for Groups to prove the following theorem, which is called the Zassenhaus (Butterfly) Lemma:

Let \(\mathrm{H}\) and \(\mathrm{K}\) be subgroups of a group \(\mathrm{G}\) and \(\mathrm{H}^{\prime}\) and \(\mathrm{K}^{\prime}\) be normal subgroups of \(\mathrm{H}\) and K, respectively. Then

i) \(\mathrm{H}^{\prime}\left(\mathrm{H} \cap \mathrm{K}^{\prime}\right) \triangleleft \mathrm{H}^{\prime}(\mathrm{H} \cap \mathrm{K})\)

ii) \(\mathrm{K}^{\prime}\left(\mathrm{H}^{\prime} \cap \mathrm{K}\right) \triangleleft \mathrm{K}^{\prime}(\mathrm{H} \cap \mathrm{K})\) iii) \(\frac{\mathrm{H}^{\prime}(\mathrm{H} \cap \mathrm{K})}{\mathrm{H}^{\prime}\left(\mathrm{H} \cap \mathrm{K}^{\prime}\right)} \simeq \frac{\mathrm{K}^{\prime}(\mathrm{H} \cap \mathrm{K})}{\mathrm{K}^{\prime}\left(\mathrm{H}^{\prime} \cap \mathrm{K}\right)} \simeq \frac{(\mathrm{H} \cap \mathrm{K})}{\left(\mathrm{H}^{\prime} \cap \mathrm{K}\right)\left(\mathrm{H} \cap \mathrm{K}^{\prime}\right)}\)

The situation can be represented by the subgroup diagram below, which explains the name ‘butterfly’.


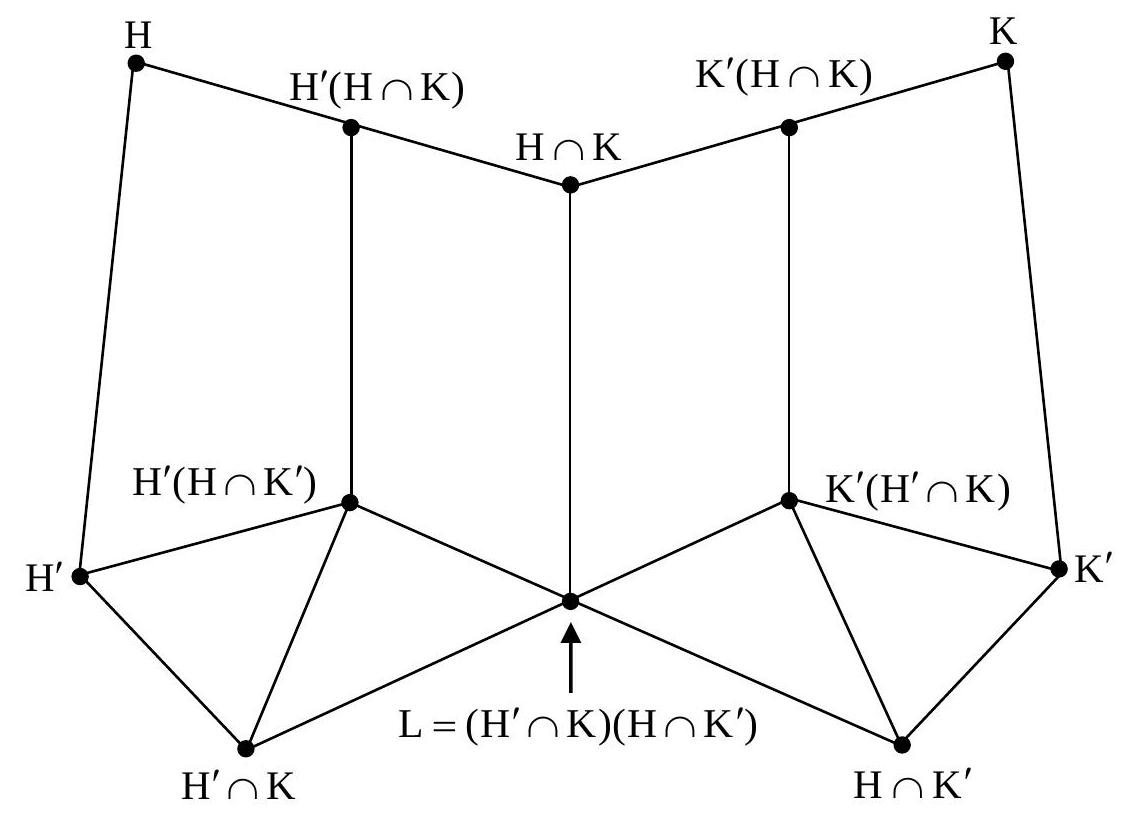
\section{PART-B (MM: 30 Marks)}

(Based on Block 3.)

5. Which of the following statements are true, and which are false? Give reasons for your answers.

i) For any ring \(R\) and \(a, b \in R,(a+b)^{2}=a^{2}+2 a b+b^{2}\).

ii) Every ring has at least two elements.

iii) If \(\mathrm{R}\) is a ring with identity and \(\mathrm{I}\) is an ideal of \(\mathrm{R}\), then the identity of \(\mathrm{R} / \mathrm{I}\) is the same as the identity of \(\mathrm{R}\).

iv) If \(\mathrm{f}: \mathrm{R} \rightarrow \mathrm{S}\) is a ring homomorphism, then it is a group homomorphism from \((\mathrm{R},+)\) to \((\mathrm{S},+)\).

v) If \(\mathrm{R}\) is a ring, then any ring homomorphism from \(\mathrm{R} \times \mathrm{R}\) into \(\mathrm{R}\) is surjective.

6. a) For an ideal I of a commutative ring \(\mathrm{R}\), define \(\sqrt{\mathrm{I}}=\left\{\mathrm{x} \in \mathrm{R} \mid \mathrm{x}^{\mathrm{n}} \in \mathrm{I}\right.\) for some \(\left.\mathrm{n} \in \mathbb{N}\right\}\). Show that

i) \(\sqrt{\mathrm{I}}\) is an ideal of \(\mathrm{R}\).

ii) \(\mathrm{I} \subseteq \sqrt{\mathrm{I}}\).

iii) \(\mathrm{I} \neq \sqrt{\mathrm{I}}\) in some cases.

b) Is \(\frac{R}{\mathrm{I}} \times \frac{\mathrm{R}}{\mathrm{J}} \simeq \frac{\mathrm{R} \times \mathrm{R}}{\mathrm{I} \times \mathrm{J}}\), for any two ideals \(\mathrm{I}\) and \(\mathrm{J}\) of a ring \(\mathrm{R}\) ? Give reasons for your answer. 7. Let \(\mathrm{S}\) be a set, \(\mathrm{R}\) a ring and \(\mathrm{f}\) be a 1-1 mapping of \(\mathrm{S}\) onto \(\mathrm{R}\). Define + and \(\cdot\) on \(\mathrm{S}\) by: \(\left.x+y=f^{-1}(f(x))+f(y)\right)\)

\(x \cdot y=f^{-1}(f(x) \cdot f(y))\)

\(\forall \mathrm{x}, \mathrm{y} \in \mathrm{S}\).

Show that \((\mathrm{S},+, \cdot)\) is a ring isomorphic to \(\mathrm{R}\).

\section{PART-C (MM: 20 Marks)}

(Based on Block 4.)

8. Which of the following statements are true, and which are false? Give reasons for your answers.

i) If \(\mathrm{k}\) is a field, then so is \(\mathrm{k} \times \mathrm{k}\).

ii) If \(\mathrm{R}\) is an integral domain and \(\mathrm{I}\) is an ideal of \(\mathrm{R}\), then Char (R)= Char (R/I).

iii) In a domain, every prime ideal is a maximal ideal.

iv) If \(\mathrm{R}\) is a ring with zero divisors, and \(\mathrm{S}\) is a subring of \(\mathrm{R}\), then \(\mathrm{S}\) has zero divisors.

v) If \(R\) is a ring and \(f(x) \in R[x]\) is of degree \(n \in \mathbb{N}\), then \(f(x)\) has exactly roots in \(\mathrm{R}\).

9. a) Find all the units of \(\mathbb{Z}[\sqrt{-7}]\).

b) Check whether or not \(\mathbb{Q}[x] /<8 x^{3}+6 x^{2}-9 x+24>\) is a field.

c) Construct a field with 125 elements.