
IGNOU MTE-10 Solved Assignment 2023 | MTE
₹201.00
Please read the following points before ordering this IGNOU Assignment Solution.
Share with your Friends
IGNOU MTE-10 Assignment Question Paper 2023
Course Code: MTE-10
Assignment Code: MTE-10/TMA/2023
Maximum Marks: 100
1. a) The equation \(x^{3}-x-1=0\) has a positive root in the interval \(] 1,2[\). Write a fixed point iteration method and show that it converges. Starting with initial approximation \(\mathrm{x}_{0}=1.5\) find the root of the equation correct to three decimal places.
b) Find an appropriate root of \(x^{3}+2 x^{2}-5=0\) in [1, 2] with \(10^{-5}\) accuracy by
i) Newton Raphson Method
ii) Secant Method
What conclusions can you draw from here about the two methods?
2. a) Using Maclaurin’s expansion for \(\sin x\), find the approximate value of \(\sin \frac{\pi}{4}\) with the error bound \(10^{-5}\)
b) Find an approximate value of the positive real root of \(\mathrm{xe}^{\mathrm{x}}=1\) using graphical method. Use this value to find the positive real root of \(\mathrm{xe}^{\mathrm{x}}=1\) correct to three decimal places by fixed point iteration method.
c) Using \(\mathrm{x}_{0}=0\) find an approximation to one of the zeros of \(\mathrm{x}^{3}-4 \mathrm{x}+1=0\) by using BirgeVieta Method. Perform two iterations.
3. a) Solve the system of equations
\[
\begin{aligned}
2 x_{1}+3 x_{2}+4 x_{3}+x_{4} & =3 \\
x_{1}+2 x_{2}+x_{4} & =2 \\
2 x_{1}+3 x_{2}+x_{3}-x_{4} & =1 \\
x_{1}-2 x_{2}-x_{3}+4 x_{4} & =5
\end{aligned}
\]
using Gauss elimination method with pivoting.
b) Find the inverse of the matrix \(\left[\begin{array}{ccc}3 & 1 & 2 \\ -2 & 3 & -5 \\ 1 & 2 & 4\end{array}\right]\) using Gauss Jordan Method.
c) Solve the following linear system \(A \mathrm{x}=\mathrm{b}\) of equations with partial pivoting
\[
\begin{gathered}
x_{1}-x_{2}+3 x_{3}=3 \\
2 x_{1}+x_{2}+4 x_{3}=7 \\
3 x_{1}+5 x_{2}-2 x_{3}=6 .
\end{gathered}
\]
Store the multipliers and also write the pivoting vectors.
4. a) Solve the system of equations
\[
\begin{aligned}
8 x_{1}-x_{2}+2 x_{3} & =4 \\
-3 x_{1}+11 x_{2}-x_{3}+3 x_{4} & =23
\end{aligned}
\]
\[
\begin{array}{r}
-x_{2}+10 x_{3}-x_{4}=-13 \\
-2 x_{1}+x_{2}-x_{3}+8 x_{4}=13
\end{array}
\]
with \(\mathrm{x}^{(0)}=\left[\begin{array}{llll}0 & 0 & 0 & 0\end{array}\right]^{\mathrm{T}}\), by using the Gauss Jacboi and Gauss Seidel method. The exact
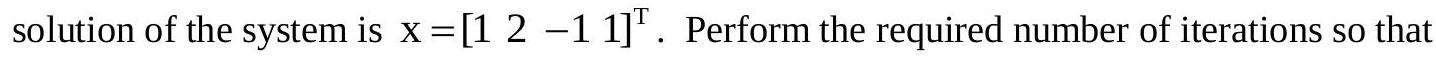
the same accuracy is obtained by both the methods. What conclusions can you draw from the results obtained?
b) Starting with \(\mathrm{x}^{(0)}=\left[\begin{array}{lll}1 & 1 & 1\end{array}\right]^{\mathrm{T}}\), find the dominant eigenvalue and corresponding eigenvector for the matrix \(A=\left[\begin{array}{ccc}4 & -1 & 1 \\ 4 & -8 & 1 \\ -2 & 1 & 5\end{array}\right]\) using the power method.
5. a) The solution of the system of equations \(\left(\begin{array}{ll}1 & 2 \\ 2 & 1\end{array}\right)\left(\begin{array}{l}x \\ y\end{array}\right)=\left(\begin{array}{c}4 \\ -2\end{array}\right)\) is attempted by the Gauss Jacobi and Gauss Seidel iteration schemes. Set up the two schemes in matrix form. Will the iteration schemes converge? Justify your answer.
b) Obtain an approximate value of \(\int_{0}^{1} \frac{\mathrm{dx}}{1+\mathrm{x}^{2}}\) using composite Simpson’s rule with \(\mathrm{h}=0.25\) and \(\mathrm{h}=0.125\). Find also the improved value using Romberg integration.
c) Find the minimum number of intervals required to evaluate \(\int_{0}^{1} \mathrm{e}^{-\mathrm{x}^{2}} \mathrm{dx}\) with an accuracy of \(\frac{1}{2} \times 10^{-4}\), by using the Trapezoidal rule.
6. a) From the following table, find the number of students who obtained less than 45 marks.
| Marks | No. of Students |
| 30−40 | 31 |
| 40−50 | 42 |
| 50−60 | 51 |
| 60−70 | 35 |
| 70−80 | 31 |
b) Calculate the third-degree Taylor polynomial about \(x_{0}=0\) for \(f(x)=(1+x)^{1 / 2}\).
c) Use the polynomial in part (a) to approximate \(\sqrt{1.1}\) and find a bound for the error involved.
d) Use the polynomial in part (a) to approximate \(\int_{0}^{0.1}(1+x)^{1 / 2} d x\).
7. a) Using \(\sin (0.1)=0.09983\) and \(\sin (0.2)=0.19867\), find an approximate value of \(\sin (0.15)\) by using Lagrange interpolation. Obtain a bound on the truncation error. b) Consider the following data
| x | 1.0 | 1.3 | 1.6 | 1.9 | 2.2 |
| f(x) | 0.7651977 | 0.6200860 | 0.4554022 | 0.2818186 | 0.1103623 |
Use Stirling’s formula to approximate \(\mathrm{f}(1.5)\) with \(x_{0}=1.6\).
c) Solve the I.V.P., \(\mathrm{y}^{\prime}=-\mathrm{y}+\mathrm{t}+1,0 \leq \mathrm{t} \leq 1, \mathrm{y}(0)=1\) using R-K method of \(0\left(h^{4}\right)\) with \(\mathrm{h}=0.1\) and obtain the value of \(y(0.2)\). Also find the error at \(t=0.2\), if the exact solution is \(y(t)=t+e^{-t}\).
8. a) The position \(f(x)\) of a particle moving in a line at various times \(x_{k}\) is given in the following table. Estimate the velocity and acceleration of the particle at \(\mathrm{x}=1.2\)
| x | 1.0 | 1.2 | 1.4 | 1.6 | 1.8 | 2.0 | 2.2 |
| f(x) | 2.72 | 3.32 | 4.06 | 4.96 | 6.05 | 7.39 | 9.02 |
b) A solid of revolution is formed by rotating about the \(x\)-axis the area bounded between \(x=0, x=1\) and the curve given by the table
| 0 | 0.25 | 0.5 | 0.75 | 1.0 | |
| f(x) | 1.0 | 0.9896 | 0.9587 | 0.9089 | 0.8415 |
Find the volume of the solid so formed using
i) Trapezodial rule ii) Simpson’s rule
c) Take 10 figure logarithm to base 10 from \(\mathrm{x}=300\) to \(\mathrm{x}=310\) by unit increment. Calculate the first derivative of \(\log _{10} \mathrm{x}\) when \(\mathrm{x}=310\).
9. a) For the table of values of \(f(x)=x e^{x}\) given by
| 1.8 | 1.9 | 2.0 | 2.1 | 2.2 | |
| f(x) | 10.8894 | 12.7032 | 14.7781 | 17.1489 | 19.8550 |
Find \(f^{\prime \prime}(2.0)\) using the central difference formula of \(0\left(h^{2}\right)\) for \(h=0.1\) and \(h=0.2\). Calculate T.E. and actual error.
b) Suppose \(f_{n}\) denotes the value of \(f(t)\) at \(t=t_{n}\). If \(f(t)=t^{3}\) then find the value of \(\frac{\left(f_{n+1}-2 f_{n}+f_{n-1}\right)}{h^{2}}\).
c) Use Runge-Kutta method of order four to solve \(y^{\prime}=x+y\). Start with \(x=1, y=0\) and carry to \(\mathrm{x}=1.5\) with \(\mathrm{h}=0.1\).
d) Find the solution of the difference equation \(y_{k+2}-4 y_{k+1}+4 y_{k}=0, k=0,1, \ldots\). Also find the particular solution when \(\mathrm{y}_{0}=1\) and \(\mathrm{y}_{1}=6\).
10. a) The iteration method
\[
x_{n+1}=\frac{1}{8}\left[6 x_{n}+\frac{3 N}{x_{n}}-\frac{x_{n}^{3}}{N}\right], n=0,1,2
\]
where \(\mathrm{N}\) is positive constant, converges to some quantity. Determine this quantity. Also find the rate of convergence of this method. b) Determine the spacing \(\mathrm{h}\) in a table of equally spaced values for the function \(f(x)=(2+x)^{4}, 1 \leq x \leq 2\), so that the quadratic interpolation in this table satisfies | error \(\mid \leq 10^{-6}\).
c) Determine a unique polynomial \(\mathrm{f}(\mathrm{x})\) of degree \(\leq 3\) such that \(f\left(x_{0}\right)=1, f^{\prime}\left(x_{0}\right)=2, f\left(x_{1}\right)=2, f^{\prime}\left(x_{1}\right)=3\) where \(x_{1}-x_{0}=h\).
MTE-10 Sample Solution 2023
Frequently Asked Questions (FAQs)
You can access the Complete Solution through our app, which can be downloaded using this link:
Simply click “Install” to download and install the app, and then follow the instructions to purchase the required assignment solution. Currently, the app is only available for Android devices. We are working on making the app available for iOS in the future, but it is not currently available for iOS devices.
Yes, It is Complete Solution, a comprehensive solution to the assignments for IGNOU. Valid from January 1, 2023 to December 31, 2023.
Yes, the Complete Solution is aligned with the IGNOU requirements and has been solved accordingly.
Yes, the Complete Solution is guaranteed to be error-free.The solutions are thoroughly researched and verified by subject matter experts to ensure their accuracy.
As of now, you have access to the Complete Solution for a period of 6 months after the date of purchase, which is sufficient to complete the assignment. However, we can extend the access period upon request. You can access the solution anytime through our app.
The app provides complete solutions for all assignment questions. If you still need help, you can contact the support team for assistance at Whatsapp +91-9958288900
No, access to the educational materials is limited to one device only, where you have first logged in. Logging in on multiple devices is not allowed and may result in the revocation of access to the educational materials.
Payments can be made through various secure online payment methods available in the app.Your payment information is protected with industry-standard security measures to ensure its confidentiality and safety. You will receive a receipt for your payment through email or within the app, depending on your preference.
The instructions for formatting your assignments are detailed in the Assignment Booklet, which includes details on paper size, margins, precision, and submission requirements. It is important to strictly follow these instructions to facilitate evaluation and avoid delays.
Terms and Conditions
- The educational materials provided in the app are the sole property of the app owner and are protected by copyright laws.
- Reproduction, distribution, or sale of the educational materials without prior written consent from the app owner is strictly prohibited and may result in legal consequences.
- Any attempt to modify, alter, or use the educational materials for commercial purposes is strictly prohibited.
- The app owner reserves the right to revoke access to the educational materials at any time without notice for any violation of these terms and conditions.
- The app owner is not responsible for any damages or losses resulting from the use of the educational materials.
- The app owner reserves the right to modify these terms and conditions at any time without notice.
- By accessing and using the app, you agree to abide by these terms and conditions.
- Access to the educational materials is limited to one device only. Logging in to the app on multiple devices is not allowed and may result in the revocation of access to the educational materials.
Our educational materials are solely available on our website and application only. Users and students can report the dealing or selling of the copied version of our educational materials by any third party at our email address (abstract4math@gmail.com) or mobile no. (+91-9958288900).
In return, such users/students can expect free our educational materials/assignments and other benefits as a bonafide gesture which will be completely dependent upon our discretion.
Related products
-
IGNOU Assignment Solution
IGNOU MPC-001 Solved Assignment 2022-2023 | MAPC | Cognitive Psychology, Learning and Memory
₹101.00 Go to the App -
IGNOU Assignment Solution
IGNOU MEG-17 Solved Assignment 2022-2023 | MEG | American Drama
₹101.00 Go to the App -
IGNOU Assignment Solution
IGNOU MEG-13 Solved Assignment 2022-2023 | MEG | WRITINGS FROM THE MARGINS
₹101.00 Go to the App






